Congress proposal 2021-031 Alteration to Appendix 1: Working Rules of the Ratings System posted on the ICCF website in the congress proposal area.
Proposed by Garvin Gray, National Delegate – Australia
Abstract
For a number of years now, there have been a lot of discussions in regards to the ICCF Rating System, and especially in regards to ICCF Rating Rule 3 and 4.
After a lot of work and assistance from many people, it is now time for a formal proposal to be made to alter Appendix 1: Working Rules of the Rating System, with particular emphasis on Rating Rules 3 and 4
Proposal:
Change the current text in the rating rules (Appendix 1) from:
3. Conversion from difference in rating D into a winning expectancy, or expected result of the game p(D):
p(D) = 1 / (1+ 10(-D/640)) for -560 ≤ D ≤ 560.
4. Conversions from percentage p into rating difference D(p):
D(p) = 640 * log10(p / (1-p)) for 0.1 ≤ p ≤ 0.9
9. The development coefficient k is used as a stabilising factor in the system:
| k = r * g | |||
| r = 10 | if R0>= 2400 | g = 1 | for gn >=80 |
| r = 70 -R0/ 40 | if 2000 < R0< 2400 | g = 1.4 – gn / 200 | for 30 < gn < 80 |
| r = 20 | if R0 <= 2000 | g = 1.25 | for gn <= 30 |
R0 the old (that is: the most recently calculated) rating of the player
gn the total number of rated games played by this player
k is rounded to 4 decimals, upwards if the 5th is 5 or higher and down otherwise
To:
3. Conversion from difference in rating D into a winning expectancy, or expected result of the game p(D):
p(D) = 1 / (1+ 10(-D/LC)) for -560 ≤ D ≤ 560.
LC = 640 * avg(SF for the two players)
SF is the player’s Strength Factor defined as follows
| SF = 2 | if R0 >= 2400 |
| SF = 1 + (R0-2000) / 400 | if 2000 < R0< 2400 |
| SF = 1 | if R0 <= 2000 |
4. Conversions from percentage p into rating difference D(p):
D(p) = LC * log10(p / (1-p)) for 0.1 ≤ p ≤ 0.9
Where D(p) is calculated for multiple games in Rules 5 and 16 the current rating of a player is not used.
In these cases the value of LC for each game is determined as follows:
LC = 640 * SF (of opponent).
The average LC for all opponents is then used to calculate D(p).
9. The development coefficient k is used as a stabilising factor in the system:
| k = r * g | |||
| r = 20 | if R0>= 2400 | g = 1 | for gn >=80 |
| r = 80 – R0/ 40 | if 2000 < R0< 2400 | g = 1.4 – gn / 200 | for 30 < gn < 80 |
| r = 30 | if R0<= 2000 | g = 1.25 | for gn <= 30 |
R0 the old (that is: the most recently calculated) rating of the player
gn the total number of rated games played by this player
k is rounded to 4 decimals, upwards if the 5th is 5 or higher and down otherwise
Change the following line in rule 8 in the rating rules (Appendix 1) from:
We= 1 / (1+ 10 (-D/640)) for -560 ≤ D ≤ 560.
To:
We = p(D) (defined in Rule 3).
These adjustments are to be made to Title Performance Requirements in 2.2 to reflect the new rating formula in Rating Rule 3.
Title Performance Requirements are based on Rating Rule 3 which define the rating performance of a player in a tournament and enables the calculation of a tournament score required to reach the necessary Title standard.
The value of LC in the formula should match the value used at the rating performance required for the Title achievement.
Change the current text in the Title regulations (Appendix 2):
a) Formula used to calculate winning expectancy (Wei)
Wei= 1/(1 + 10-(Rp-Ri)/640 )
To:
a) Formula used to calculate winning expectancy (Wei)
Wei= 1/(1 + 10-(Rp-Ri)/LC )
LC is the variable defined in Rating Rule 3. The value of LC is calculated with both player ratings set to the rating value of the performance requirement to meet the Title requirement.
Rationale
Why do current Rating Rules 3 and 4 need to be changed?
Rating Rule 3 does not state the correct probability of a player winning a game against another player with a different rating. This applies to higher rated players.
As a result players playing a game against a higher rated player receive an unfair advantage.
Players playing a game against a lower rated player have an unfair disadvantage.
Most players know this as they try to play in tournaments above their rating.
This proposal recommends a higher rating constant of 1280 for players above 2400.
There are two reasons for choosing this value.
1) It is a good fit with the actual data in the games database.
2) If this value had been used over the last 10 years then the number of players rated above 2600 would have remained constant at 1.0%.
A more detailed description follows in the form of questions with detailed responses.
What is the true winning expectancy?
The published ICCF games database is available for download from the website. The number of wins in the database can be compared to the number of wins expected from the formula in Rating Rule 3. In general Rating Rule 3 claims that players are winning twice as many games as they actually are winning in practice.
An example: There are 1585 games in the ICCF games database that meet the criteria of a rating difference of between 91 and 110 rating points. This if for games dated between 2015 and 2018. The formula in Rating Rule 3 claims that the higher rated player should have approximately 282 (net) wins from those games. There are only 94 (net) wins for the higher rated player.
Games in the ICCF Database with one player over 2450.
| Rating Difference | Number of games in the ICCF database | Number of wins in the ICCF database | Wins expected using Rating Rule 3 |
|---|---|---|---|
| 20(10-30) | 4362 | 56 | 157 |
| 40(31-50) | 3563 | 71 | 256 |
| 60(51-70) | 2780 | 90 | 299 |
| 80(etc) | 2239 | 87 | 320 |
| 100 | 1585 | 94 | 282 |
| 120 | 1182 | 100 | 251 |
| 140 | 895 | 82 | 221 |
| 160 | 678 | 104 | 190 |
| 180 | 471 | 88 | 147 |
| 200 | 396 | 97 | 137 |
Why should the winning expectancy match the data in the Games Database?
Players will have their rating adjusted based on how they perform compared to other similar rated players. If a player performs better than expected then their rating should go up. If they perform worse than expected then their rating should go down. Rating Rule 3 states that a player should win one game out of six against a player 100 rating points lower. The example above shows that for this group of games the higher rated player is only winning one game out of fifteen. The higher rated players will be seen as performing badly and have their rating reduced. This will occur even though they are performing at the expected level.
An example: George plays in a semi-final tournament against 12 other players. His rating is 100 points higher than the average of his opponents. Rating rule 3 claims that George will win two games against his opponent on average. But the data in the Games Database shows that George is expected to only win one game. Because George only wins one game he loses 5 rating points.
What data is used from the ICCF Games Database?
The file titled “Server Complete until 31-12-2020” can be downloaded from the ICCF website from the ICCF Games Archive.
From this file all games with a date between Jan 2015 and Dec 2018 were extracted. The start date of the tournament is used in the heading of each game. This period has been chosen so that all games from tournaments are likely to be chosen. Using the end date for games would have led to many tournaments having only partial inclusion of games.
What is rating deflation?
Because higher rated players often play against lower rated players they will lose rating points. The example of George above demonstrates this. Rating deflation has been occurring over recent decades. The draw rate has been increasing and the winning expectancy defined in the ICCF rules has not been adjusted for this.
The following table shows the number of players in the higher rating groups.
| Players | 2005 | 2009 | 2014 | 2019 |
| > 2600 | 80 | 61 | 42 | 20 |
| > 2550 | 236 | 191 | 124 | 79 |
| > 2500 | 549 | 409 | 294 | 205 |
Why is rating deflation a problem?
Access to the GM Title has become very difficult. This will also gradually become a problem for the IM and SIM Titles.
As the higher rated players have their ratings fall, the lower rated players will also have their ratings fall.
The higher rated players will fall to 2400. This will make it very difficult for other players to reach 2400.
How many rating points have been incorrectly lost by higher rated players?
There are 20075 games in the selection of games evaluated in this proposal for players with one player above 2450 and the other player within a range of 350 rating points. Of those games the higher rated player had a total of 1196 net wins.
The current rating system with LC=640 predicts that the higher rated player would win 2717 of those games. This is an over prediction of 1521 games. As a result of not winning the correct number of predicted games the higher rated players were unfairly worse off by 5 rating points for each of those 1521 games that were not won. This has resulted in a unfair loss of 1521*5 = 7605 rating points for the higher rated players.
A value of LC=1280 predicts that 1383 games should be won by the higher rated players. This is still above the actual number of wins and would still have resulted in a loss of rating points by higher rated players. The loss would have been 187*5 = 935 rating points. This may suggest an even higher value of LC is needed however the model must be balanced over various rating ranges.
Why should the k factor be 20 for ratings above 2400?
Currently the k factor is 10. The value of a draw was decreased in 2016 when a new rating formula was introduced. This would slow the rate at which a player could progress to their proper rating. This proposal further reduces the value of the draw. The impact of a draw on a players rating would now be half that of what occurred before 2016. By increasing the k factor from 10 to 20 this would balance the changes. The value of a win would also double. Wins are much harder to achieve and it is appropriate that wins have a greater impact to a player’s rating.
Why should the k factor be 30 for ratings below 2000?
The k factor needs to be higher for lower rated players. When players start playing correspondence they typically improve over time and their rating increases. They frequently retire with a higher rating than they started with. For this reason the change in rating for the lower rated player in a game needs to be more than the change in rating for the higher rated player. The range of k factor, also called acceleration factor, used to be between 10 and 20. This proposal changes it to a range of 20 to 30. It will increase the value of wins which have become harder for all players.
How will higher rated players benefit?
Deflation will cease. High rated players will be able to play in many more tournaments without unfairly losing rating points. By adjusting the requirements to achieve Titles there will be many more Titles issued.
Currently there is a very small number of GM Titles awarded because the current rating equation requires players to win an unreasonable number of games.
How will lower rated players benefit?
If higher rated players have their ratings fall then this will create a ceiling for all players. The ICCF Rules mention the link to FIDE ratings more than 20 times. ICCF ratings will maintain a level of compatibility to FIDE ratings.
Players can expect to find many higher rated players joining open tournaments. This will give new players to the ICCF a greater chance to demonstrate their skills and progress their ratings at a faster level.
What is the evidence for a change in the parameter LC in rating Rule 3?
Graphs are given in Appendix B below showing actual winning performance and predicted winning performance using different rating constants. These graphs are created for players at different rating levels. The data, in table form, that these graphs are created from can be provided on request. It is all reproducible from downloaded games from the ICCF website.
What is the Strength Factor in the formula?
The winning expectancy varies with player ratings. So the value of LC must vary and increase as a player’s rating increases. This increase is implemented by multiplying the current rating constant of 640 by a variable that increases with player strength. Players rated above 2400 have more draws due to engine use. So the number 640 needs to be multiplied by the factor 2. This will give a value of LC of 1280 for these players. Players with ratings below 2000 will continue to use the current rating constant of 640.
What is the average taken of Strength Factor in the formula?
The average of player strength for the two players is taken so that the winning expectancy adds to 1.0. Having the winning expectancy add to 1.0 is considered to be a fundamental requirement of a rating system.
In practice this will still not occur. In 2012/1 the ICCF rating system was changed to use the maximum of a player’s initial and current rating when calculating the opponents winning expectancy. This proposal does not address this issue. It is important that this proposal stands alone and recommends a formula that has winning expectancy add to 1.0 for an individual game.
A consequence of using the average strength factor is that the value of LC for players in the range 2000 to 2400 will be higher for games against players rated above them and lower for games against players rated lower than them. This is a more accurate match with the data.
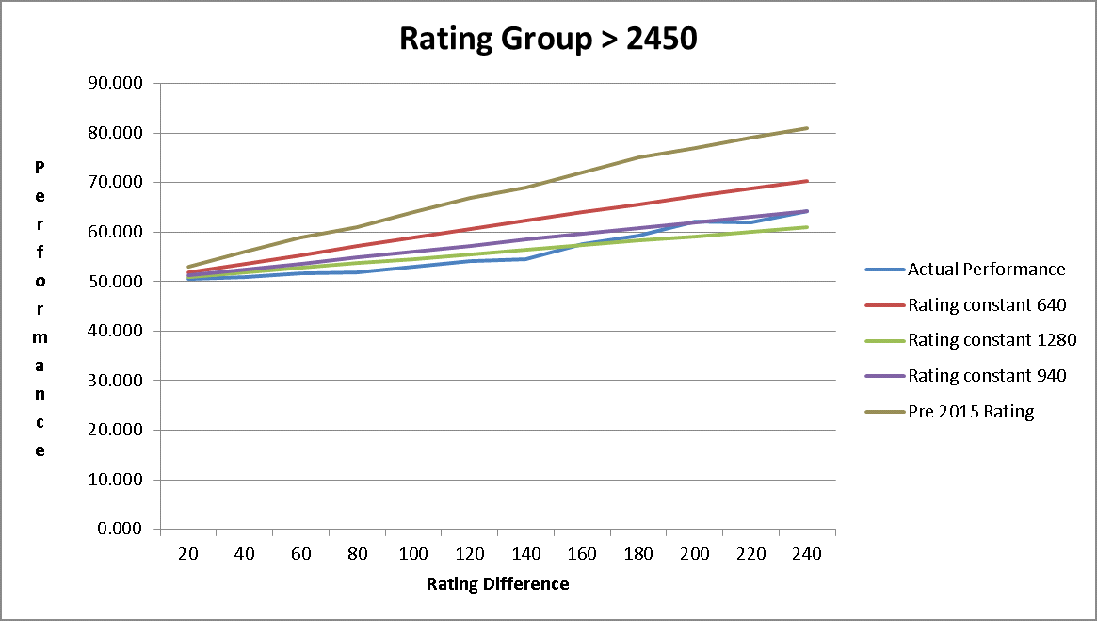
Why is the value of 1280 chosen for players with ratings above 2400?
Using the proposed formula the effective value of LC would be 1280 where both players have ratings above 2400. For a small rating difference the data shows that a higher value of 1500 is needed. The games that fit into this category will be between players all above 2400. For rating differences of 200 a lower value of LC provides a better fit. Most of the games used in the analysis at this rating difference involved a player being less than 2400. By using the average LC of the two players a better fit is achieved for winning expectancy between the two players.
The value of 1280 is the best estimate of LC to be accurate for games between high rated players and also between high and lower rated players.
It is recognised that increased engine use and more powerful engines will require an even higher value for LC in the future. There will need to be periodic reviews to address this.
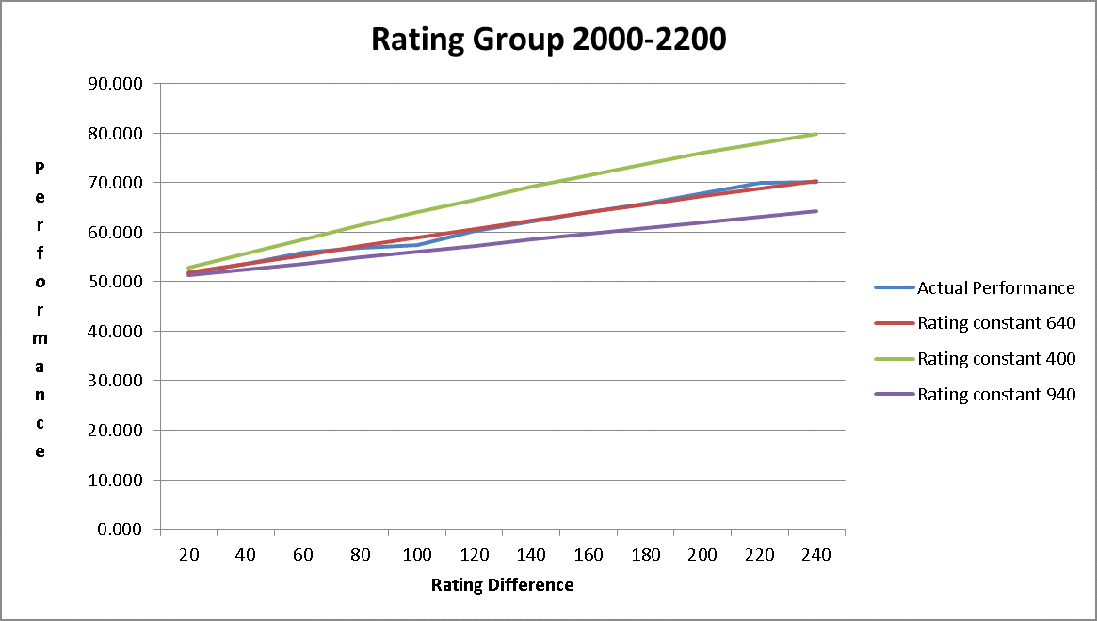
What should the value of LC be for players below 2000?
The graph clearly shows the value 400 as a good fit for the rating constant LC . This is somewhat misleading. New players are typically given a start rating of 1800 and rapidly increase as they discover how to best use chess engines. This rapid rise results in scores that outperform their ratings by a big margin. The best way to address this issue is to use a higher initial rating for new players. This topic is beyond the scope of this proposal but should be reviewed in the future.
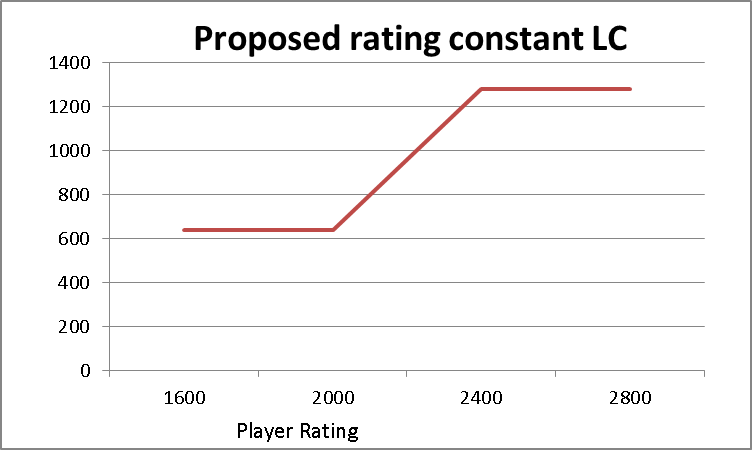
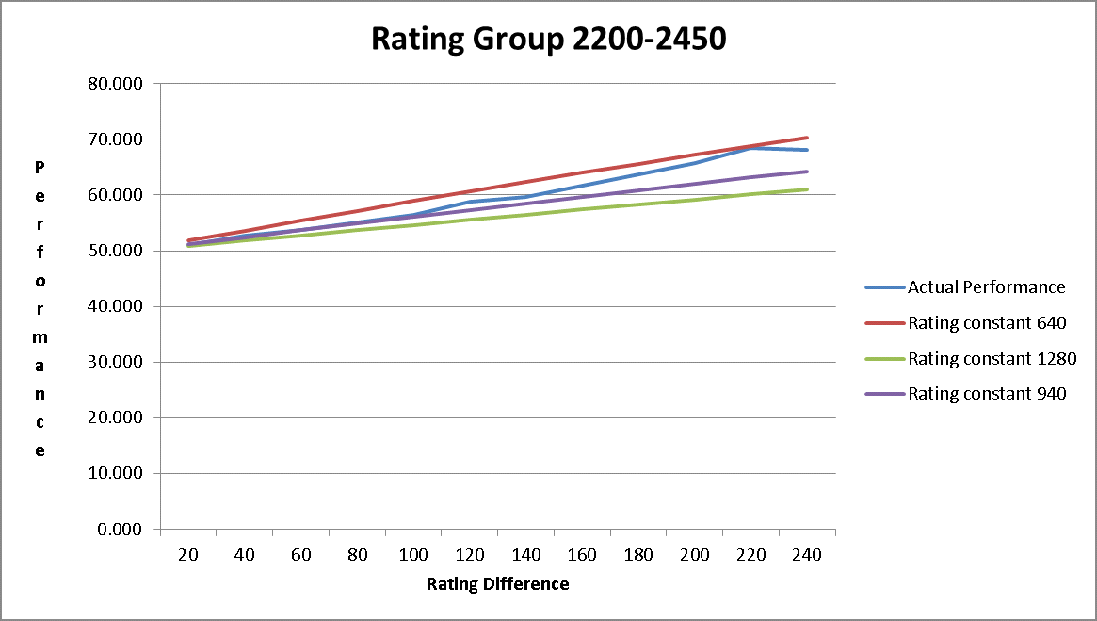
What should the value of LC be for players between 2000 and 2400?
The rating constant LC must change uniformly between player ratings of 2000 and 2400. Otherwise there would be very different outcomes in rating adjustments for only a small change in a players rating. That would encourage players to manage their ratings at the end of a rating period. The following graph shows how the rating constant changes between 2000 and 2400.
See the graphs below “Proposed Rating Constant LC” in Appendix A.
What would have happened if this change to the rating formula had been made 10 years?
A dynamic chart is available that shows that how the distribution of ratings would have changed over the last 10 years if this proposal had been implemented in 2011. See the next clause for details of where to access this chart and how to use it.
Using this chart it can be demonstrated that the number of players rated greater than 2600 (i.e. the GM level) would have increased a small amount over the last 10 years. The chart shows that the current number of players rated over 2600 has fallen to 0.4% using the existing rating system.
The chart also shows that the number of players with ratings above 2450 would have increased significantly using the proposed rating formula. This would be a reasonable and expected outcome with the engine assistance that players have been developing. The current rating formula has resulted in a fall from 10.2% to 7.8% of players rated above 2450.
It would be impossible to replace current ratings with those predicted by this dynamic chart. Over future years the distribution of ratings will move slowly to towards the ratings distribution predicted by this modelling.
Aspirational players have been unable to achieve higher ratings because the rating system is unfair. Achieving a high rating is also made more difficult when the strongest players have had their ratings fall by so much over the last 10 years. The fall in ratings of the strongest players has created a barrier preventing other players from reaching a high rating.
How to use the dynamic chart that shows the distribution of ratings over the last 10 years.
The following link connects to a dynamic ratings chart that shows how the distribution of ratings would have occurred under different rating systems.
https://iccfratingslab.z35.web.core.windows.net/
. Along the horizontal x axis are ratings groups of width 100.
. Along the vertical y axis is shown the fraction of players that occur in each of these groups.
. To view how the distribution of ratings have actually occurred over the last 10 years and compare to what would have happened with the rating system in this proposal follow these instructions:
. Click the line box for “Current ICCF Ratings” and “Proposal”
. The data can be presented with the Bar option if this is preferred to the Line option.
. Move the blue circle (with the mouse or arrow keys) on the line under the graph to the far left so that the rating period 2011/3 is shown.
. Move the blue circle to the right and view how the distribution of ratings changes over time.
How will a change in the rating constant LC affect Title awards?
Winning expectancy determines how well a player is performing. Using the current rating formula, a win against 6 other players of the same strength is considered to be a performance of 100 points higher. Using the value of 1280 for the rating constant will mean that a win against 12 other players of the same strength will be considered to be a performance of 100 points higher. This is a fairer system given that wins are much more difficult to achieve when most players have the support of a 3400 rated engine.
Why not set the value of the draw to zero?
This would be equivalent to using a rating constant of infinity. This would create new problems. Players would only want to play against much lower rated players. This way they could gradually gain points with wins with a much lower risk of losing a game.
How will the changes affect my rating?
An online rating calculator has been created. This calculator enables two ratings to be inserted. The calculator will show the change in rating for a Win, Draw or Loss for each player. The rating change under the current and proposed rating formula will be displayed.
http://www.metrochessclub.org.au/ICCF/ICCF.html
What if the rating formula is not changed?
Deflation will continue to occur. Titles will not be awarded. Those players that play against lower rated players will continue to have their rating fall faster than players that play against opponents of the same strength. Many players attempt to find ways around the error in the rating formula and this would continue.
APPENDIX A: Proposed Rating Constant LC
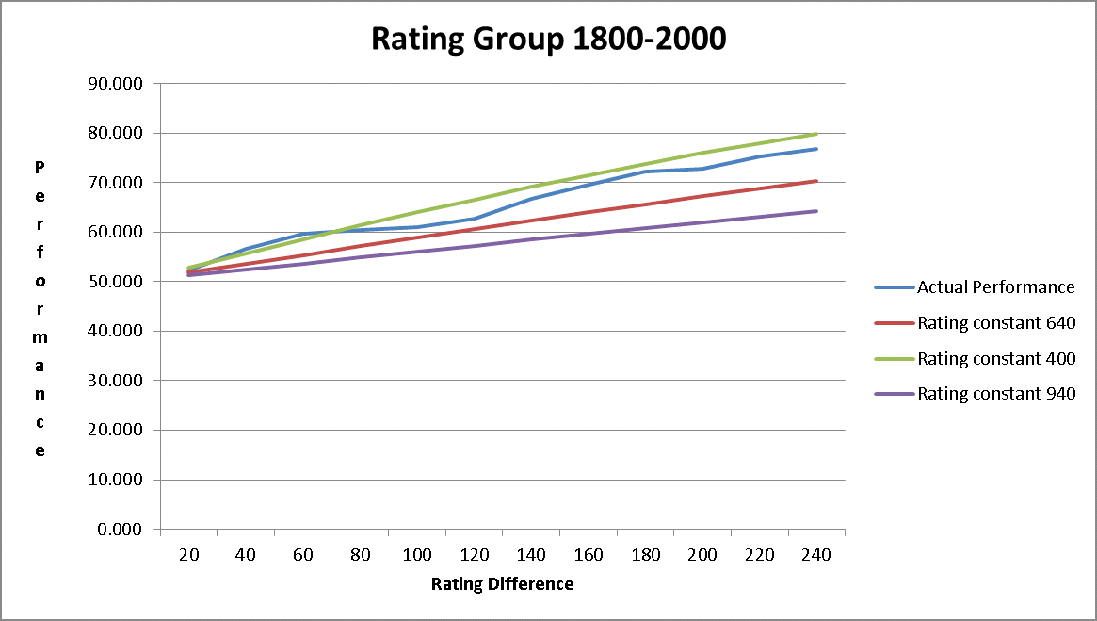
APPENDIX B: Actual Performance versus Winning Expectancy.
These graphs show the actual performance of players at increasing rating difference. The predicted winning expectancy is given for different values of the rating constant LC.
Games are included in a rating group if one of the players belongs in that rating range. Some games are included in two different groups if the two players are in different rating groups.
These charts show the average winning expectancy of players over all games. An average of the winning expectancy for the two players is used in the calculation for the winning expectancy for an individual game. This is to ensure that the winning expectancies for an individual game add to 1.0.
Assessment
A lot of assessment has already gone into creating the groundwork for this proposal. It is anticipated that this proposal will be able to be implemented by either the 2022/2 or 2022/3 rating period.
Effort
The Rating Rules will need to be updated. It is possible that some paid ICCF officials will need to consulted to ensure correct implementation. This is only a possibility as this opportunity has existed for a number of years already, but I thought it should be mentioned as this could result in a cost outlay for ICCF.
Considerations
This proposal will take some time to implement as it will be involving changes to one of the most fundamental areas in ICCF.
Documentation
All documentation that needs to be changed has already been provided in the proposal section.
Comments
14.07.2021 Austin Lockwood
As ICCF Services Director, I was extremely interested to read this proposal.
The proposers are quite correct to note that there is a problem with the current ratings system for many of the reasons they mention (and others). I am grateful to them for bringing this to the attention of our members by proposing some interesting modifications to the current system.
I was however concerned by the apparent lack of expert statistical review, the rather cavalier approach to determining system parameters, and the lack of optimisation against known game outcomes. Indeed, earlier versions of the proposal had some rather obvious flaws, for example the sum of winning expectancies was not equal to one in some cases. To their credit, the proposers fixed this particular issue when it was pointed out to them, however it did feel like a last minute „tweak” rather than an acknowledgement that such a fundamental requirement of a probabilistic rating system had been overlooked.
However, I am personally no more qualified to comment on these issues than the proposers, so to present a completely objective, expert, and unbiased opinion of this proposal, I requested an independent review by one of the world’s leading experts in this field, Professor Mark Glickman.
Professor Glickman’s comments are here.
In summary, although there are some valuable ideas in this proposal, I cannot support it in it’s current form; much more work is required, and I urge delegates to vote against this proposal and instead support Proposal 2021-033.
Austin Lockwood
ICCF Services Director
17.07.2021 Garvin Gray
The purpose of this proposal is to provide relief for players resulting from the incorrect winning expectancies currently claimed in Rating Rule 3 that incorrectly adjust ratings after each rating period. Two incorrect claims made must be corrected immediately. Further comments may be made upon review by Professor Glickman after further consideration. Priority will be given to addressing concerns expressed by National Delegates.
Proposal proponents have been aware that winning expectancies have not added up to 1.0 since 2012/1. The use of the maximum of initial and current rating for an opponent causes this. Austin Lockwood and Professor Glickman should have been aware of this as a result of the 2016 review and the many studies of the rating system undertaken since then. Delegates supported this change in 2011 and no attempt has been made to correct this. Proposal proponents did make a change at the suggestion of Professor Glickman over this issue. Jeff Sonas had already discussed this issue with the proponents one month earlier.
It has been claimed that the increase in rating constant would result in serious inflation. The evidence in the report is based on using the higher rating constant of 1280 for game data going back to 2011 when the draw rate was much higher. This approach is flawed as the higher rating constant is totally inappropriate for 2011. Analysis of inflation from the dynamic chart demonstrates that inflation would be negligible by implementation time of 2022. The trend suggests that an even higher rating constant will be required in a few years to avoid further deflation.
It is recommended to National Delegates that this proposal be accepted. It will provide immediate relief to players. The proposal proponents strongly support the concept of a review of correspondence chess under the scenario of a rapidly increasing draw rate resulting from engine use. With the diversity of player views that exist it may take much longer than one year to complete. This review might cover tournament styles, time controls and even the game itself. This proposal should not be rejected. There are no harmful effects and only considerable benefits from accepting this proposal.
17.07.2021 Per Söderberg
First of all, I’m not qualified to judge the ideas and formulas expressed in this proposal or the wise words from Mr Glickman. (I’m MSc in Physics.)
And as I see how my own rating decreases by each draw I play with lower rated players, I do feel this is a big problem, have I really lost so much of my playing strength as the rating system says? OK, I have also lost about 100 ELO-points in FIDE. But, in FIDE, it is that I get older and am not as fast thinking, as I used to be. In CC this shouldn’t matter. Of course, my belief is that it is due to stronger playing engines.
And, at least, we need to increase the interest to play in ICCF events by making sure that the rating system is fair.
But my question is why we can’t first vote in favour of this proposal and see if it helps and then still have the proposal 2021-033 to evaluate and enhance the rating system further?
If we agree on this then we can vote in favour of both. The formulas as presented here shouldn’t be worse that the present formulas. If I would be so bold to suggest that the possibility to vote in favour of both is made possible! I can’t see that they are excluding each other in every aspect. If we start by going in the right direction and then fix any possible error made by a more thorough analysis?
Amici Sumus,
Per Söderberg
17.07.2021 Gino Franco Figlio
Dear Per,
Garvin and Gordon circulated this proposal among delegates and officers for months before they are now published.
It is not a free improvement for higher rated players, it is an improvement based on negative consequences for the mid rated players using Gordon’s own analysis.
That is why I believe prospective observation as described in proposal 2021-033 is better than experimenting with players’ ratings with this proposal since we know it is not fair for everyone. I am using fair in the sense that it hinders some players for the benefit of the higher rated.
18.07.2021 Garvin Gray
Dear Per,
Thank you for your comment.
A small correction in my previous comment is required – It has been claimed that the increase in rating constant would result in serious inflation. The evidence in the report is based on using the higher rating constant of 1280 for game data going back to 2011 when the draw rate was much 'higher’.
wording should be – when the draw rate was much 'LOWER’. Typo slipped in.
18.07.2021 Garvin Gray
Gino,
The problem is not passed onto the lower rated players. In fact they benefit.
1) Lower rated players will have a higher k factor so that they can progress more quickly to a stable rating.
2) Lower rated players will have the benefit of the chance to progress above 2400 and higher. Currently all the higher rated players are deflating to 2400.
3) Lower rated players will have the benefit of higher rated players willing to play in tournaments with them.
At an early stage Gordon Dunlop thought that mid-range ratings might fall with a higher rating constant. The dynamic chart suggests otherwise, although it is very difficult to determine based on the rapidly increasing draw rate at various levels.
18.07.2021 Austin Lockwood
Dear Garvin,
I should just point out that the data used to generate the dynamic chart is also the data on which Professor Glickman based his analysis; you seem to be asking us to accept the validity of the former but reject the later?
Austin
18.07.2021 Per Söderberg
Dear Gino,
For sure, I was not contacted about this until it showed up as proposal 2021-029 – now removed. And I’m a delegate. Btw, who is Gordon? It’s not Gordon Anderson I presume.
Right now the system is flawed as the winning expectancy and the real winning results differs quite a lot! And this favours the lower rated player in each game. The current system with the increase of draws, beyond the expectancy, is making the rating difference to go in the direction of a middle rating. Look at the World Championship, one player qualified for a final winning one game! Or the Olympiads, very few games are decided.
This is the current situation, agree?
This is the core of the problem, we need to adopt the rating so that it reflects the true winning expectancy. When I read this, it seems to be the aim of this proposal. Is it correct? We wouldn’t know until we have tried it!? That is how man gets forward – solve a problem by propose something we believe to be true. Trial and error, a child need to crawl to learn how to walk.
It is negative for the mid rated player, you claim, my question is compared to what? The present system? The present system is unfair to the higher rated in every game. If I play versus a player with 200 rating points less, the expectancy tells that I shall win every second game and the others end in draw to keep the rating level. The fact is that I draw with these players.
And of course, the norms are also based on the incorrect winning expectancy. And there are very few who can earn a GM-norm. Not like in the past.
Now if this proposal does improve the present system, then we can very well support it. And at the same time, we can also support 2021-033 to enhance the system even further. Now we are told that if we approve this proposal then there will be no more enhancement of rating and norms? May I say that I don’t see why not?
18.07.2021 Austin Lockwood
Dear Per,
I should explain why 2021-031 and 2021-033 are conflicting.
Implementing any rating system on the server involves considerable investment, both in terms of money and professional and volunteer time; so yes, we could ignore the expert advice we have been given and spend tens of thousands of Euros implementing this system on the server… maybe for 2022/3 or 2022/4, and a few months later implement a new system based on the conclusions of 2021-033, repeating this considerable expense and work for all concerned.
But this would be a poor approach; implementing both proposals is not an option. Delegates must choose between:
1. a system which has been described by one of the leading experts in this field as „a patchwork approach”, making „strong and unjustified assumptions”, and „not consistent with basic data science principles”, and which has been shown empirically to do the opposite of the very thing it claims to do (improve the relationship between rating difference and game outcome) to be implemented in the summer of 2022 at the earliest, or,
2. a system which has been built from the ground up, customised for ICCF and fine-tuned to the pattern of results we have in correspondence chess, based on sound statistical principals, and to be implemented perhaps six months later.
Austin
18.07.2021 Austin Lockwood
Dear Per,
We don’t need to implement a system to investigate it’s effects; we already have the data from game outcomes, we can apply any rating algorithm we like to these data and look out the hypothetical outcome.
The scientific approach is to do the experiments in the lab before taking the risk of implementing something live.
We have done this, and we have given these data to the world’s leading expert on chess ratings; his conclusion was that the formula very slightly improved the relationship between rating and game outcome for elite players (but not significantly so), but it was worse for ordinary players.
Garvin appears to be challenging the methodology used by Professor Glickman PhD.
Austin
18.07.2021 Per Söderberg
Dear Austin,
Thanks for your explanation. I see the point made. I also would like to see a strong and well grounded system rather than today’s situation.
Perhaps it would be a good thing if we can compare the statistical skills of Garvin and Gordon, before dismissing their work as „patchwork”.
In my mind new ideas may be worth considering! Once at the Royal Institute of Technology, I had a teacher who got famous for solving an unsolvable integral, he said: „I didn’t know that it wasn’t solvable, so I solved it.”
Best Regards, Per
PS To me it looks like only the constants and formulas needs to have old numbers to be replaced with new ones. As an object oriented programme shall be made!? And thus I didn’t see that the implementation would take so much effort!
18.07.2021 Per Söderberg
Dear Austin,
We may be out of phase with the replies here. I posted a reply to your first message addressed to me. Of course, we must test and check the outcome of the new formulas suggested by Garvin and Gordon, before implementing them. I understood from the proposal that this was claimed to be done by them? And you also have to test the implementation before using it. That goes without saying!
These are principles I use in my everyday work. Would never let something go to the customer without assuring that it is correct. Doing so would backfire and put me out of business.
Do we know that Gordon is not a professor and PhD in statistics?
Also I do understand that the elite players will have very little effect by these proposed formulas. As they play mostly with each others! They would not play in an event with low category. I have failed to find players to invitationals because they offer a too low category. Rating points are important to the elite players.
All the best, Per
Voting Summary
A vote of YES will mean that this proposal will pass. Players winning expectancies will now start to get closer to their actual percentage score. Players will have greater opportunities to play in higher category tournaments and therefore more norm opportunities.
A vote of NO will mean the current rating system will remain. Rating deflation will contain to be an issue and the number of higher category tournaments will continue to reduce in number.
A vote of ABSTAIN is not a vote but means the vote holder has no opinion and does not wish to represent the correspondence chess players of his or her federation in this matter.
========
Updated 2021-07-18
