The ICCF Rating system
by Nol van ’t Riet (NED), updated by Gerhard Binder (GER) and Mariusz Wojnar (POL)
One of the eternal questions, which arises regularly in every kind of sport, is whether for instance, the first World Champion ever would have been a better player than the present one. In our sport of correspondence chess, we could put forward questions like: was the first World Champion (1953) Cecil Purdy from Australia, better than the one who has most recently been crowned, Jan Timmerman (NED) or ICCFs own “Mister World Championships” Prof. Dr. Vladimir Zagorovsky, from the former USSR, who became World champion in 1965? Or was Hans Berliner (USA) the best correspondence chess player ever, after his win with 14 points out 16 games in 1968 in the 6th World Championship Final? Or player who has scored the most Grandmaster norms ever, at the moment record-holders gained 13 norms each: Achim Soltau (GER) and Guillermo F. Toro Solís de Ovando (CHI)? Or Tonu Õim (EST) and Joop van Oosterom (NED), the only players to win two World Championships? Or is present leader of the ICCF rating list, Nikolai Papenin (UKR), although he has not yet won the World Championship?
In order to be able to answer questions like these, the American professor Arpad Elo (born near Papa in Hungary in 1903) developed the so-called ELO Rating system for the over-the-board chess world. He worked on it during the fifties and sixties and in 1970 it was accepted by FIDE. The system not only gives the opportunity to compare players from different times, but can also be used for another, much more important purpose. Since 1950 FIDE and since 1959, ICCF have awarded players with titles like Grandmaster and International Master. A rating system is an objective basis to award titles to players for equal achievements.
The German word for Grandmaster (Großmeister) appears for the first time in the preface of the 1907 Ostend tournament book, written by the German winner of the tournament Siegfried Tarrasch. The word was used for the six strongest players who competed against each other four times in a separate section, called the Grandmaster tournament: Tarrasch, Schlechter, Marshall, Janowski, Burn and Chigorin. Until 1950 the chess world used the words International Master and Grandmaster for the players who were regularly invited to international events, respectively for the best players in the world. According to this tradition the former World champion Max Euwe was always addressed by his Dutch pupils (like Jan Hein Donner) with the French version of the word Grandmaster: ‘Grand-maître’.
In 1950 the World chess federation FIDE started to bestow the International Master and Grandmaster titles. Both titles bear some analogy to the academic degree doctor: they are awarded for a once demonstrated skill and after their bestowal they are valid for life. In 1959 the first ICCF titles were bestowed. The first Grandmasters were Olaf Barda (NOR), Lucius Endzelins (AUS), H. Malmgren (SWE), Mario Napolitano (ITA), Cecil J.S. Purdy (AUS) and Lothar Schmid (GER; at that time FRG). The title of International Master was awarded to: František Batík (CSR), Valt Borsony (CSR), Sten Isaksson (SWE), Jaroslav Ježek (CSR), Sv. Kjellander (SWE), George R. Mitchell (ENG) and Leopold Watzl (AUS). There were no rules, the players received titles for their performances in World Championship finals and other strong tournaments.
Eight years later, at the 1967 ICCF Congress at Krems, the first rules for the awarding of the titles were adopted. To make rules it was necessary to be able to compare the achievement of one player in a certain tournament with those of other players in other tournaments. So one had to replace the then subjective standards by more objective norms. The biggest problem one has to solve therefore is that the score of a player in a certain tournament is an insufficient indicator. This strength can only be assessed if there is a norm with which the strength of that special tournament can be measured.
It is clear, therefore, that one has to look at the individual playing strength of all single participants of the tournament. The 1967 ICCF Title rules therefore made use of the number of title holders who participated in the tournament. In order to express the difference in playing strength between the players, according to these rules, they were divided into three groups: the Grandmasters, the International Masters and the others. Within such a group all players were supposed to be of equal strength. The strength of a tournament and the title norms belonging to it were appointed on account of the number of participants in each of these three groups. In this manner one, for instance, had to score (on the average) for a Grandmaster title norm 50% against the Grandmasters, 70% against the International Masters and 80% against the others. In 1980 these percentages were raised respectively to 55%, 75% and 85% to make the gain of a title more difficult.
Meanwhile the insight grew that this system had several shortcomings. Ever stronger the question came up to discriminate the playing strength of a tournament in a better way. That is to say: no more based on only three groups of players of equal mutual strength, but based on the individual playing strength of all individual players. And it was just to solve this problem that for more than twenty years professor Arpad Elo had developed his rating system. This system uses mathematical and statistical methods to express differences in playing strength by using numbers (the so-called ratings). Because of its scientific origin (the supposition that differences in playing strength are normally distributed) an ELO-system is completely different from for instance the ATP ranking in tennis, which is not based on any statistical theory at all.
Since the 1976 ICCF Congress at Bucharest a working group Rating system of the ICCF has worked on the building of its own rating system by making the work of Elo usable for international correspondence chess. From 1976 until 1980 Raimo Lindroos (FIN) led this group. From 1980 until 1989 Nol van ’t Riet (NED) was the chairman of the working group.
When he took over the work at the 1980 ICCF Congress at Linz, the then ICCF President Hans-Werner von Massow -who was not very much in favour of ratings- said to him: ‘You have to build a rating system for ICCF, because many people want to have it, and I want you to do this, although I think and I hope you will never succeed’. At the 1987 ICCF Congress in Bloemendaal, the last of the Presidency of Hans-Werner von Massow, the ICCF rating system was unanimously (!) accepted, together with the ICCF Rating System Administrative Rules.
On the list valid at the 1987 ICCF Congress at Bloemendaal the top five players were: 1. Dr. Jonathan Penrose (ENG – 2700); 2. Luís Santos (POR – 2690); 3. Erik Bang (DEN – 2650); 4. Ju. M. Kotkov (URS – 2650); 5. I. A. Kopilov (URS – 2640).
At that time there were 8,752 players incorporated in the databank, who had finished 132,422 games. On the list there were 2,353 players with a fixed rating (which is a rating based on 30 or more games). Ratings at that time were rounded off to nearest multiple of five.
Games of all kind of international tournaments (of Master Class and higher tournament levels) since 1950 have been incorporated in the system. One had to go back for such a long period as it normally takes tens of years before a correspondence chess player has finished enough games to get a statistically reliable rating. It can be proved that the rating of a player who has finished at least 30 games has a certain degree of reliability. Therefore in the ICCF system, those ratings are called fixed ratings.
The history of the building of the ICCF Rating system has been described in the Report of the working group to the 1986 ICCF Congress at Baden. In 1989, at the ICCF Congress at Richmond, the working group was replaced by an expert group and, as a member of that group, Nol van ’t Riet became the first ICCF Ratings commissioner. In 1994 he was replaced by his successor Gerhard Binder (GER) who started a tremendous job by modernising the software infrastructure, the input procedures and the output of the ICCF Rating system.
On the list valid until 30.09.2012 the top five players are: 1.Nikolai Papenin (UKR) 2715; 2.Joop van Oosterom (NED) 2711; 3.Joachim Neumann (GER) 2692; 4.Ron Langeveld (NED) 2688; 5.Roman Chytilek (CZE) 2682.
At this time (09.06.2012) there are 40 413 players incorporated in the databank, 1 645 of them women. The published main list contains 6 620 (active) players with a rating based upon at least 12 games each, and with a last result which was recorded after 2008. Since 1998 the ratings are rounded to the nearest integer.
A nice aspect of ratings is that one can compare the past and the present. Below you will find some of these comparisons. The first one gives for the years 1955 until March 2012 the five players with the highest rating. It is surprising to see that only 47 players have been in the top five during these 57 years.
| Year | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1955 | Schmid | Arnlind | Lundqvist | Koch | Balogh |
| 2630 | 2470 | 2460 | 2435 | 2430 | |
| 1958 | Schmid | Endzelins | Arnlind | Lundqvist | Napolitano |
| 2605 | 2480 | 2470 | 2460 | 2460 | |
| 1960 | Schmid | O’Kelly | Nielsen | Arnlind | Lundqvist |
| 2620 | 2525 | 2495 | 2480 | 2475 | |
| 1962 | Schmid | Husák | Nielsen | Lundqvist | Endzelins |
| 2620 | 2525 | 2510 | 2500 | 2495 | |
| 1964 | Schmid | Husák | Zagorovsky | Nielsen | Rittner |
| 2620 | 2525 | 2525 | 2515 | 2500 | |
| 1965 | Schmid | Arnlind | Husák | Nielsen | Zagorovsky |
| 2620 | 2545 | 2525 | 2515 | 2515 | |
| 1966 | Schmid | Ericsson | Zagorovsky | Arnlind | Husák |
| 2620 | 2555 | 2550 | 2545 | 2545 | |
| 1967 | Ericson | Zagorovsky | Arnlind | Husák | Nielsen |
| 2555 | 2550 | 2545 | 2545 | 2540 | |
| 1968 | Ericson | Zagorovsky | Arnlind | Husák | Nielsen |
| 2555 | 2550 | 2545 | 2545 | 2540 | |
| 1969 | Berliner | Gulbrandsen | Husák | Zagorovsky | Arnlind |
| 2735 | 2595 | 2565 | 2550 | 2545 | |
| 1970 | Berliner | Gulbrandsen | Husák | Arnlind | Zagorovsky |
| 2735 | 2595 | 2565 | 2550 | 2550 | |
| 1971 | Berliner | Husák | Zagorovsky | Endzelins | Nielsen |
| 2765 | 2625 | 2625 | 2615 | 2610 | |
| 1972 | Berliner | Zagorovsky | Husák | Endzelins | Nielsen |
| 2765 | 2650 | 2625 | 2615 | 2610 | |
| 1973 | Berliner | Zagorovsky | Husák | Endzelins | Nielsen |
| 2765 | 2650 | 2625 | 2615 | 2610 | |
| 1974 | Berliner | Husák | Endzelins | Zakharov | Nielsen |
| 2765 | 2625 | 2615 | 2615 | 2610 | |
| 1975 | Endzelins | Zakharov | Nielsen | Arnlind, Rittner |
Zagorovsky |
| 2615 | 2615 | 2610 | 2605 | 2605 | |
| 1976 | Hollis | Arnlind | Zagorovsky | Zakharov | Rittner |
| 2625 | 2620 | 2620 | 2615 | 2610 | |
| 1977 | Hollis | Arnlind | Zagorovsky | Zakharov | Vaisman |
| 2625 | 2620 | 2620 | 2615 | 2615 | |
| 1978 | Palciauskas | Khasin | Arnlind | Hollis | Richardson |
| 2665 | 2655 | 2625 | 2625 | 2615 | |
| 1979 | Palciauskas | Khasin | Hollis | Arnlind | Richardson |
| 2665 | 2655 | 2635 | 2625 | 2615 | |
| 1980 | Palciauskas | Khasin | Hollis | Arnlind | Richardson |
| 2665 | 2655 | 2635 | 2625 | 2615 | |
| 1981 | Sloth | Palciauskas | Khasin | Hollis | Zagorovsky |
| 2700 | 2655 | 2645 | 2635 | 2635 | |
| 1982 | Sloth | Palciauskas | Khasin | Hollis | Zagorovsky |
| 2700 | 2655 | 2645 | 2635 | 2635 | |
| 1983 | Sloth | Khasin | Arnlind | Bang | Dubinin |
| 2700 | 2670 | 2625 | 2625 | 2625 | |
| 1984 | Sloth | Khasin | Arnlind | Bang | Richardson& Govbinder |
| 2700 | 2670 | 2625 | 2625 | 2610 | |
| 1985 | Sloth | Khasin | Molchanov | Arnlind | Bang |
| 2700 | 2685 | 2635 | 2625 | 2625 | |
| 1986 | Bang | Khasin | Molchanov | Sloth | Deuel |
| 2650 | 2645 | 2640 | 2640 | 2625 | |
| 1987 | Penrose | Santos | Bang | Kotkov | Kopilov |
| 2700 | 2690 | 2650 | 2650 | 2640 | |
| 1988 | Penrose | Lapienis | Santos | Svenson | Umansky |
| 2715 | 2710 | 2690 | 2680 | 2675 | |
| 1989 | Lapienis | Penrose | Santos | Umansky | Svenson |
| 2715 | 2715 | 2690 | 2675 | 2665 | |
| 1990 | Lapienis | Penrose | Santos | Umansky | Svenson |
| 2715 | 2710 | 2690 | 2675 | 2665 | |
| 1991 | Penrose | Lapienis | Santos | Umansky | Bang |
| 2715 | 2715 | 2690 | 2680 | 2650 | |
| 1992 | Penrose | Umansky | Santos | Bang | Svenson |
| 2719 | 2689 | 2685 | 2678 | 2668 | |
| 1993 | Penrose | Umansky | Bang | Santos | Timmerman |
| 2724 | 2696 | 2677 | 2676 | 2664 | |
| 1994 | Penrose | Timmerman | Umansky | Santos | Bang |
| 2718 | 2708 | 2694 | 2684 | 2678 | |
| 1995 | Timmerman | Penrose | Umansky | Santos | Bang |
| 2724 | 2711 | 2698 | 2686 | 2675 | |
| 1996 | Timmerman | Penrose | Umansky | Santos | Bang |
| 2726 | 2711 | 2701 | 2680 | 2675 | |
| 1997 | Timmerman | Penrose | Umansky | Neumann | Santos |
| 2724 | 2711 | 2701 | 2693 | 2680 | |
| 1998 | Timmerman | Penrose | Neumann | Oosterom | Umansky |
| 2727 | 2711 | 2693 | 2687 | 2687 | |
| 1999 | Timmerman | Penrose | Neumann | Oosterom | Elwert |
| 2738 | 2711 | 2696 | 2684 | 2681 | |
| 2000/1 | Timmerman | Penrose | Oosterom | Neumann | Santos |
| 2743 | 2711 | 2711 | 2681 | 2680 | |
| 2000/2 | Timmerman | Oosterom | Elwert | Rause | Santos |
| 2747 | 2713 | 2685 | 2684 | 2680 | |
| 2001/1 | Timmerman | Oosterom | Rause | Neumann | Tarnowiecki |
| 2744 | 2719 | 2689 | 2684 | 2679 | |
| 2001/2 | Timmerman | Oosterom | Rause | Tarnowiecki | Elwert |
| 2734 | 2714 | 2708 | 2692 | 2687 | |
| 2002/1 | Andersson | Timmerman | Oosterom | Rause | Tarnowiecki |
| 2741 | 2730 | 2724 | 2717 | 2692 | |
| 2002/2 | Andersson | Timmerman | Oosterom | Rause | Tarnowiecki |
| 2741 | 2733 | 2724 | 2721 | 2692 | |
| 2003/1 | Berliner | Andersson | Timmerman | Oosterom | Rause |
| 2751 | 2736 | 2733 | 2725 | 2720 | |
| 2003/2 | Andersson | Oosterom | Timmerman | Berliner | Rause |
| 2736 | 2735 | 2735 | 2726 | 2723 | |
| 2004/1 | Oosterom | Andersson | Timmerman | Berliner | Rause |
| 2748 | 2737 | 2734 | 2726 | 2710 | |
| 2004/2 | Oosterom | Andersson | Berliner | Timmerman | Elwert |
| 2754 | 2737 | 2726 | 2723 | 2717 | |
| 2005/1 | Oosterom | Andersson | Berliner | Elwert | Timmerman |
| 2777 | 2737 | 2726 | 2717 | 2706 | |
| 2005/2 | Oosterom | Andersson | Berliner | Elwert | Neumann |
| 2779 | 2737 | 2726 | 2724 | 2712 | |
| 2006/1 | Oosterom | Andersson | Elwert | Berliner | Neumann |
| 2779 | 2737 | 2727 | 2726 | 2717 | |
| 2006/2 | Oosterom | Andersson | Elwert | Berliner | Neumann |
| 2776 | 2737 | 2727 | 2726 | 2716 | |
| 2007/1 | Oosterom | Andersson | Berliner | Elwert | Neumann |
| 2776 | 2737 | 2726 | 2725 | 2714 | |
| 2007/2 | Oosterom | Andersson | Berliner | Elwert | Neumann |
| 2771 | 2737 | 2726 | 2716 | 2712 | |
| 2008/1 | Oosterom | Andersson | Berliner | Elwert | Davletov |
| 2741 | 2737 | 2726 | 2719 | 2707 | |
| 2008/2 | Oosterom | Andersson | Berliner | Elwert | Davletov |
| 2745 | 2737 | 2726 | 2724 | 2707 | |
| 2009/1 | Oosterom | Elwert | Davletov | Schön | Langeveld |
| 2735 | 2724 | 2707 | 2696 | 2694 | |
| 2009/2 | Oosterom | Elwert | Davletov | Schön | Langeveld |
| 2732 | 2724 | 2707 | 2696 | 2694 | |
| 2009/3 | Oosterom | Elwert | Davletov | Timmerman | Langeveld |
| 2736 | 2724 | 2707 | 2698 | 2697 | |
| 2010/1 | Oosterom | Elwert | Davletov | Langeveld | Schön |
| 2741 | 2724 | 2707 | 2702 | 2699 | |
| 2010/2 | Oosterom | Elwert | Davletov | Schön | Langeveld |
| 2737 | 2724 | 2707 | 2699 | 2696 | |
| 2010/3 | Oosterom | Elwert | Davletov | Schön | Neumann |
| 2725 | 2724 | 2707 | 2699 | 2695 | |
| 2010/4 | Elwert | Oosterom | Davletov | Schön | Langeveld |
| 2724 | 2722 | 2707 | 2699 | 2696 | |
| 2011/1 | Oosterom | Langeveld | Schön | Papenin | Neumann |
| 2712 | 2699 | 2699 | 2693 | 2692 | |
| 2011/2 | Oosterom | Papenin | Schön | Neumann | Chytilek |
| 2712 | 2708 | 2699 | 2692 | 2690 | |
| 2011/3 | Papenin | Oosterom | Schön | Neumann | Chytilek |
| 2733 | 2711 | 2699 | 2692 | 2689 | |
| 2011/4 | Papenin | Oosterom | Schön | Neumann | Chytilek |
| 2741 | 2708 | 2699 | 2692 | 2687 | |
| 2012/1 | Papenin | Oosterom | Neumann | Chytilek | Langeveld |
| 2729 | 2708 | 2692 | 2685 | 2681 | |
| 2012/2 | Papenin | Oosterom | Neumann | Langeveld | Chytilek |
| 2723 | 2711 | 2692 | 2688 | 2682 | |
| 2012/3 | Papenin | Oosterom | Neumann | Langeveld | Chytilek |
| 2715 | 2711 | 2692 | 2688 | 2682 | |
| 2012/4 | Oosterom | Papenin | Neumann | Langeveld | Chytilek |
| 2711 | 2707 | 2692 | 2687 | 2683 | |
| 2013/1 | Oosterom | Papenin | Langeveld | Chytilek | Dronov |
| 2711 | 2692 | 2689 | 2685 | 2676 | |
| 2013/2 | Oosterom | Langeveld | Papenin | Chytilek | Dronov |
| 2711 | 2688 | 2687 | 2685 | 2676 | |
| 2013/3 | |||||
Among those 47 players there are 36 players whose name has been more than one time in the top five.
Players in this list for the longest periods are:
| Name | Country | Years | from | to | |
|---|---|---|---|---|---|
| 1 | Hans Berliner | USA | 40 | 1969 | 2008 |
| 2 | Eric Arnlind | SWE | 31 | 1955 | 1985 |
| 3 | Vladimir Zagorovsky | URS | 19 | 1964 | 1982 |
| 4 | Lucius Endzelins | AUS | 18 | 1958 | 1975 |
| 5 | Gert-Jan Timmerman | NED | 17 | 1993 | 2009 |
| 6 | Julius Nielsen | DEN | 16 | 1960 | 1975 |
| 7 | Joachim Neumann | GER | 16 | 1997 | 2012 |
| 8 | Joop van Oosterom | NED | 16 | 1998 | 2013 |
| 9 | Erik Bang | DEN | 14 | 1983 | 1996 |
| 10 | Jonathan Penrose | ENG | 14 | 1987 | 2000 |
| 11 | Luís Santos | POR | 14 | 1987 | 2000 |
| 12 | Karel Husák | CSR | 13 | 1962 | 1974 |
| 13 | Horst Rittner | GDR | 13 | 1964 | 1976 |
| 14 | Lothar Schmid | FRG | 12 | 1955 | 1966 |
| 15 | Hans-Marcus Elwert | GER | 12 | 1999 | 2010 |
| 16 | Mikhail Umansky | RUS | 11 | 1988 | 1998 |
These are the names of the players who have been leading in the correspondence chess world in the second half of the 20th and the beginning of 21st centuries. To be in the top five for ten or more years means to you must have devoted almost your whole life to correspondence chess.
Another interesting list is the list of the players with the highest ratings ever:
| Name | Country | Rating | Year | |
|---|---|---|---|---|
| 1 | Joop van Oosterom | NED | 2779 | 2005 |
| 2 | Hans Berliner | USA | 2765 | 1971 |
| 3 | Gert-Jan Timmerman | NED | 2747 | 2000 |
| 4 | Ulf Andersson | SWE | 2741 | 2002 |
| 5 | Nikolai Papenin | UKR | 2741 | 2011 |
| 6 | Hans-Marcus Elwert | GER | 2727 | 2006 |
| 7 | Jonathan Penrose | ENG | 2724 | 1993 |
| 8 | Olita Rause | LAT | 2723 | 2003 |
| 9 | Joachim Neumann | GER | 2717 | 2006 |
| 10 | Donatas Lapienis | LIT | 2715 | 1989 |
| 11 | Jalil Davletov | RUS | 2709 | 2006 |
| 12 | Kenneth Frey | MEX | 2703 | 2003 |
| 13 | Wolfram Schön | CAN | 2703 | 2008 |
| 14 | Ron Langeveld | NED | 2702 | 2010 |
| 15 | Mikhail Umansky | RUS | 2701 | 1996 |
| 16 | Jørn Sloth | DEN | 2700 | 1981 |
Looking at the ratings in the first table one might get the feeling that there is a kind of inflation in the ICCF rating system, as the ratings of the top players are nowadays higher than they were thirty years ago. In 1994 as part of his study at The Hague University one of the members of the expert group, Jeroen Alingh Prins (NED), investigated a possible deflation or inflation in the ICCF rating system. A group of 295 players was constructed who had already finished at least 80 games in 1986 and who have been active in the years after. All kind of statistical surveys on these data made clear that there was no indication for inflation or deflation at all. That is to say: the average rating of the players in this group was quite the same over the years.
It’s important to realise that the group of players in the system increased from 167 in 1950 via 8,752 in 1987 to 31,050 in 2002 and up to 39 784 in 2011. This means that in every range of ratings there will be more players with a rating in that specific range. So that’s why also at the verges of the system there will be more players with a high (or a low) rating. So it’s not a matter of inflation, but a matter of spreading of the ratings.
The most important feature of ratings is that they are corrected when a player ends new games. These changes are essentially illustrated in the chart below. For example the final of the 10th World championship has been taken. This tournament has been carried through from 1979 until 1984.
| Name | Country | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|---|
| 1 | Palciauskas | USA | 2665 | 129 | 67% | 10½ | 11½ | 2675 |
| 2 | Morgado | ARG | 2495 | -41 | 44% | 7 | 10½ | 2530 |
| 3 | Richardson | ENG | 2615 | 79 | 61% | 9½ | 10 | 2620 |
| 4 | Sanakoev | URS | 2535 | -1 | 50% | 7½ | 10 | 2560 |
| 5 | Kauranen | FIN | 2560 | 24 | 53% | 8 | 8½ | 2565 |
| 6 | Maeder | FRG | 2555 | 19 | 53% | 8 | 8½ | 2560 |
| 7 | Muhana | ARG | 2490 | -46 | 44% | 7 | 8 | 2500 |
| 8 | Govbinder | URS | 2610 | 74 | 60% | 9 | 8 | 2600 |
| 9 | Boey | BEL | 2580 | 44 | 56% | 8½ | 8 | 2575 |
| 10 | Kletsel | URS | 2545 | 9 | 51% | 8 | 7½ | 2540 |
| 11 | Seeliger | FRG | 2565 | 29 | 54% | 8½ | 6½ | 2545 |
| 12 | Estrin | URS | 2560 | 24 | 53% | 8 | 5½ | 2535 |
| 13 | Svenningsson | SWE | 2405 | -131 | 32% | 5 | 5 | 2405 |
| 14 | Sørensen | DEN | 2470 | -66 | 41% | 6½ | 4½ | 2450 |
| 15 | Engel | FRG | 2430 | -106 | 36% | 5½ | 4½ | 2420 |
| 16 | Kalish | USA | 2500 | -36 | 45% | 7 | 3½ | 2465 |
The real procedure is slightly more complicated than outlined below. The simplifications that have been made have the intention of explaining more clearly the thoughts behind the rating calculations. The order of the players is according to the points they scored at the end. These can be found in column 5.
Column 1 gives the ratings of the players at the start of the tournament. Using these ratings one can calculate that the average rating is 2536. This number indicates the strength of the tournament. It also makes it possible to compare this strength with those of other tournaments. The final of the 11th World Championship for instance had a rating of 2520, the final of 12th a rating of 2531, the final of the 15th a rating of 2556. In column 2 you find the difference of each player with average rating. A minus sign indicates the rating of this player is below the average. With the differences from column 2 the most important part of the calculation starts. Differences are looked up in the table below. This table gives the ‘expected score’ in percentages, for everybody.
| rating | score (%) | rating | score (%) | rating | score (%) | rating | score (%) |
|---|---|---|---|---|---|---|---|
| difference | H L | difference | H L | difference | H L | difference | H L |
| 0 – 3 | 50 50 | 92 – 98 | 63 37 | 198 – 206 | 76 24 | 345 – 357 | 89 11 |
| 4 – 10 | 51 49 | 99 – 106 | 64 36 | 207 – 215 | 77 23 | 358 – 374 | 90 10 |
| 11 – 17 | 52 48 | 107 – 113 | 65 35 | 216 – 225 | 78 22 | 375 – 391 | 91 9 |
| 18 – 25 | 53 47 | 114 – 121 | 66 34 | 226 – 235 | 79 21 | 392 – 411 | 92 8 |
| 26 – 32 | 54 46 | 122 – 129 | 67 33 | 236 – 245 | 80 20 | 412 – 432 | 93 7 |
| 33 – 39 | 55 45 | 130 – 137 | 68 32 | 246 – 256 | 81 19 | 433 – 456 | 94 6 |
| 40 – 46 | 56 44 | 138 – 145 | 69 31 | 257 – 267 | 82 18 | 457 – 484 | 95 5 |
| 47 – 53 | 57 43 | 146 – 153 | 70 30 | 268 – 278 | 83 17 | 485 – 517 | 96 4 |
| 54 – 61 | 58 42 | 154 – 162 | 71 29 | 279 – 290 | 84 16 | 518 – 559 | 97 3 |
| 62 – 68 | 59 41 | 163 – 170 | 72 28 | 291 – 302 | 85 15 | 560 – 619 | 98 2 |
| 69 – 76 | 60 40 | 171 – 179 | 73 27 | 303 – 315 | 86 14 | 620 – 735 | 99 1 |
| 77 – 83 | 61 39 | 180 – 188 | 74 26 | 316 – 328 | 87 13 | over 735 | 100 0 |
| 84 – 91 | 62 38 | 189 – 197 | 75 25 | 329 – 344 | 88 12 |
For Richardson, you find in column 2 a rating difference of + 79 rating points with the average of his opponents in this tournaments. As he is supposed to be stronger than this average opponent he is expected to score over 50%. The above table points out that a rating difference of + 79 rating points belongs to a positive (H: higher) score of 61%. So Richardson was expected to score 61% against his 15 opponents. Column 3 gives this expected percentage score for each player. Column 4 shows the score in game points (rounded upwards) corresponding to that percentage score. So Richardson was expected to score 9½ from 15 games
In column 5 you find the real scores in the tournament. Comparing the columns 4 and 5 shows that Palciauskas not only was expected to win the tournament, but he did with one point more than expected. To him that was rather appropriate, as Morgado and Sanakoev particularly, had played much better as could be expected on account of their start ratings. Columns 4 and 5 also show that Seeliger, Estrin, Sørensen and Kalish achieved a disappointing score.
After the tournament is finished the difference between the expected score (column 4) and the real score (column 5) is used to calculate a new rating for each player. This difference is multiplied by 10 and with that result the old rating is increased or decreased, according to the fact if the player has scored above or under his expectation. Column 6 holds the thus calculated new ratings.
As indicated above, real calculations are somewhat more complicated. We mention the following differences:
- § it is possible that at the beginning of a tournament some players still do not have a rating as they haven’t already finished enough games. The rating rules contain a procedure to give those players temporarily a provisional rating
- § in reality, the expected score of column 4 is calculated as the sum of expected scores in all single games. No rounding offs are carried through
- § sometimes another number is taken instead of the 10 that is used to multiply the score difference with in order to calculate a new rating. This depends on the number of games someone has already played and also on the value of his old rating
- § if a player has scored extremely above (Morgado and Sanakoev) or under (Estrin and Kalish) his expectation extra rating points are added or subtracted. The reason why is that an exceptional result could indicate that the start rating of the player was no longer adequate. Therefore it is important to steer the player quickly towards a proper rating
- § tournaments like the above mentioned World Championship may last many years. Some games are finished very rapidly, others take four or five years. Some players participate in the meantime in other tournaments, some players don’t. In order to rate results of those differences in a proper way, all players get a new rating each year. Therefore it is done as if the player has played in a tournament with just those opponents with which he ended a game in that particular year.
Not all players are equally pleased with their own ratings. During the years of the construction of the ICCF rating system it has very often appeared that lots of players have their own subjective view on their own playing strength and on those of others.
One is often inclined to hang up ones own playing strength on that one best result one has achieved many years ago. The majority of less good results are forgotten. In this respect it is worth remarking that a rating system only counts the full and half points and zeros which a player achieves. Not illness, lack of time, personal problems, blunders, writing errors, sacrifices for the team, nor brilliant insights – and no matter in which tournament the win of player A against player B was achieved: the win is a win, whether the game was played in a World Championship final or in a friendly country match.
For CC players who are used to playing lots of tournaments at the same time, ratings are not so pleasant. For in the ratings are also included the results of the games which were played with less effort. To Palciauskas (see above) this meant that his rating in the list of 01.01.1984 was not 2675, but only 2430, because in the same period in which he won the World Championship he also participated in the final of the 2nd ICCF World Cup with the result of 3 in 16 games against an average rating opposition of 2333.
It was hoped that the adoption of a rating system in ICCF would reduce the phenomenon of players not trying their best in some tournaments, or withdrawing from others.
Ratings – rules improvement adopted by ICCF Congress 2011 in Finland
Information presented below comes mostly from the ICCF Congress minutes.
Rating Commissioner Gerhard Binder (GER) during ICCF Congress 2011 in Järvenpää (Finland) conducted a working group for all those interested delegates prior to his official report as the topic was highly technical and perhaps not everyone wanted to sit through the details. The following was discussed (round of experts and then with delegates):
At previous Congresses, I always had to report strange cases abusing the concept of start ratings. Already in 2010, I checked some variants to avoid such problems and to improve the system. However, I was not able to present a proper solution to the Congress in Kemer. Additional statistical research was necessary to find out what is the best-suited formula for the difference of ratings, which is the base for the evaluation of a game.
Since 2000, we are using the difference in the start ratings of both players, independent from their rating development during the game. This was a logical method to ensure that all games of a tournament were treated equally whenever they were finished. However, with ongoing time the concept was criticized more and more, not only due to the mentioned strange cases. For new players, especially in open tournaments, the start ratings were sometimes too low and damaged the rating of higher rated opponents who often refused therefore to participate in Cups or Jubilee tournaments.
After some simulations and discussing five possible solutions especially with my deputy Mariusz Wojnar, I favoured the idea to use the recent published rating for the player and the higher value of start rating and recent rating for the opponent.
Using newest ratings for the calculation is of course the most accurate method following the theory of Prof. Elo and near to the thinking of the players. It works fine, if a tournament is finished within a short time and is evaluated before the next tournament starts (OTB). In CC we have a totally other situation. The results of a tournament come in over different periods and other tournaments are played simultaneously. This may lead to strange distortion for the players in one tournament, especially if an opponent drops down dramatically due to withdrawals in other events. The current situation is also unjust if the opponent’s start rating does not correspond to his real strength and he goes up during the tournament due to good performance. To use the better value (start rating, recent rating) is a good compromise to reduce such injustice. Of course, such a choice for a higher value has hidden dangers for the balance of the system (inflation).
To estimate this danger and to further convince Mariusz and myself (and with a tremendous amount of time!) I made step by step a complete recalculation of all rating lists from 2000/1 (when the start-rating concept was introduced) to 2011/3 using this proposal. This comprised 28 rating lists with all players who finished at least one game during that period (18 443 players). After removing those players who do not have a published rating in 2011/3 13 492 players remained. Analysing their rating performances convinced me that this way of calculating the rating difference does not produce inflation but, on the contrary, rather compensates the existing deflation.
Presentation of this simulation was given at Congress which of excerption is placed below.
===
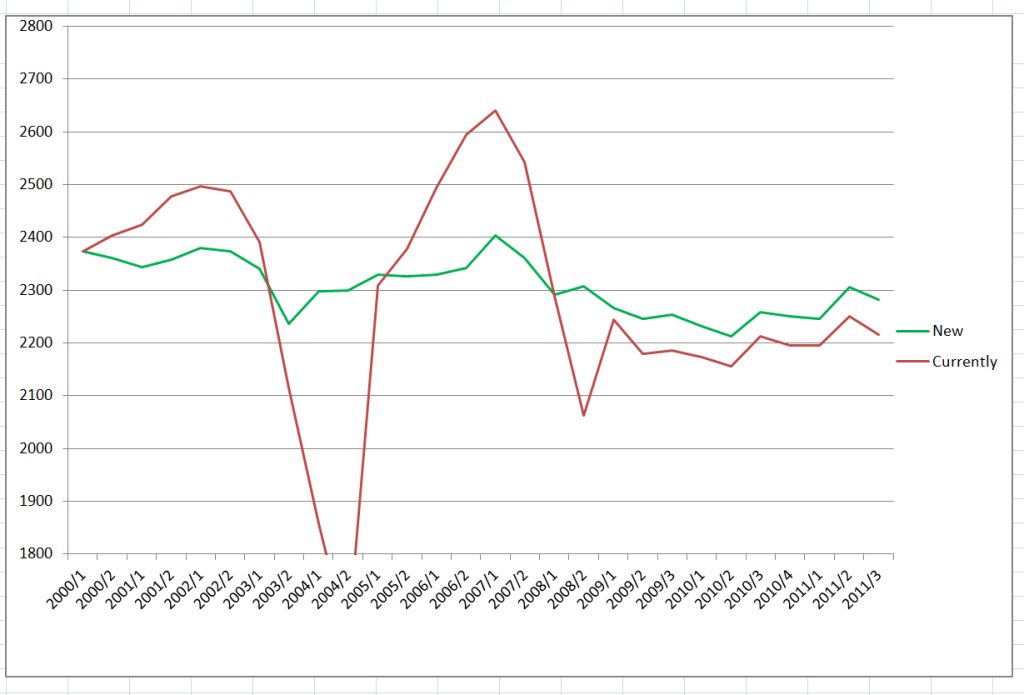
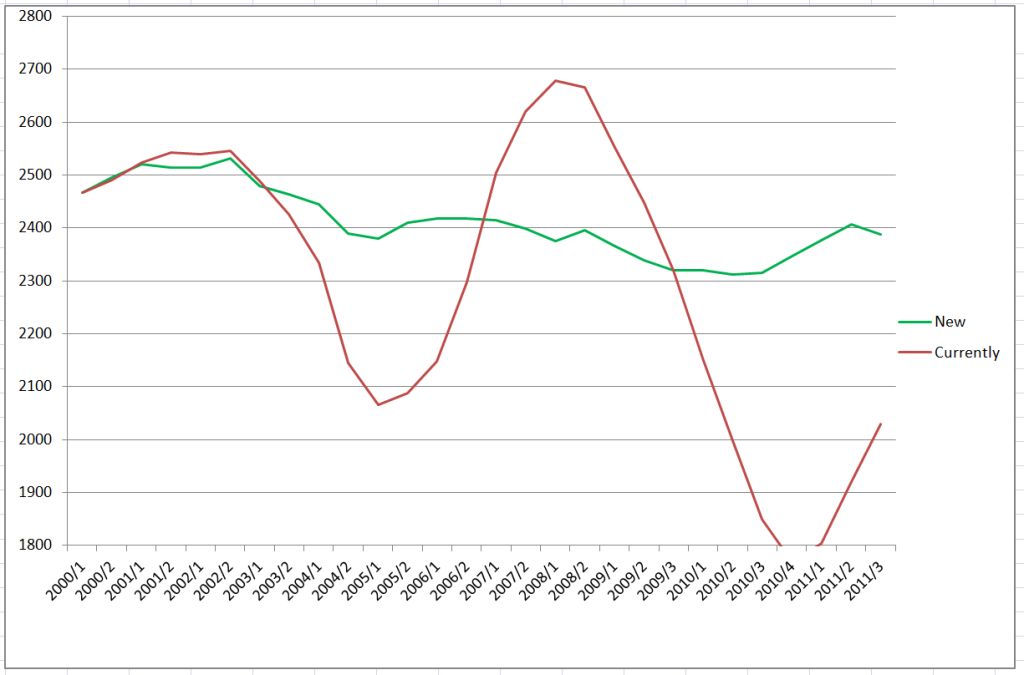
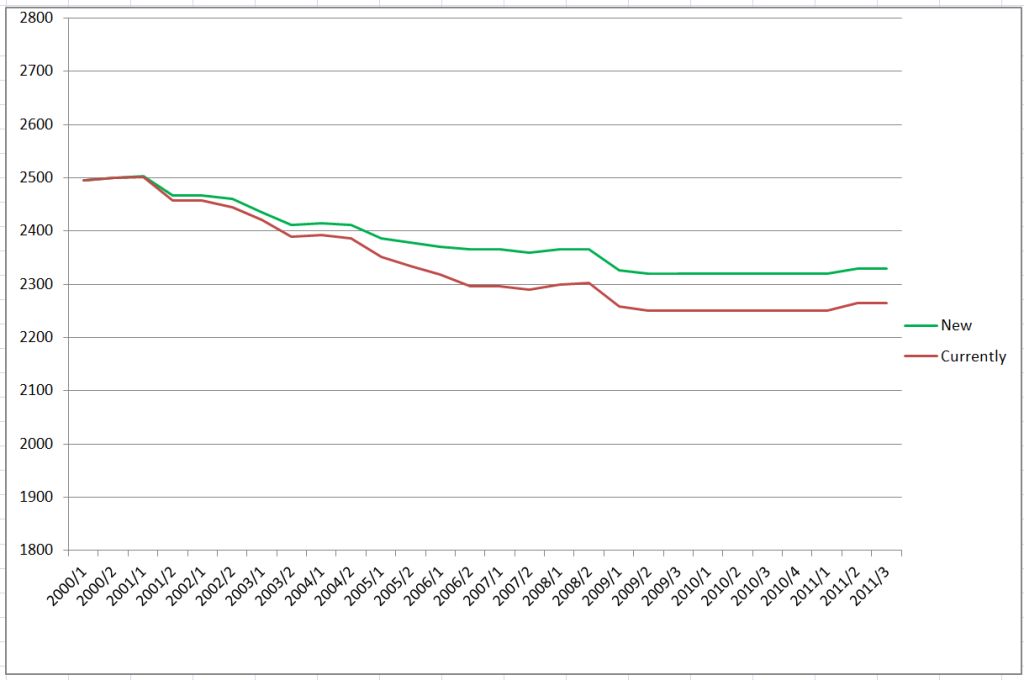
Charts ilustrating Gerhard’s analysis
Development of average ratings for the period from 2000 to 2011
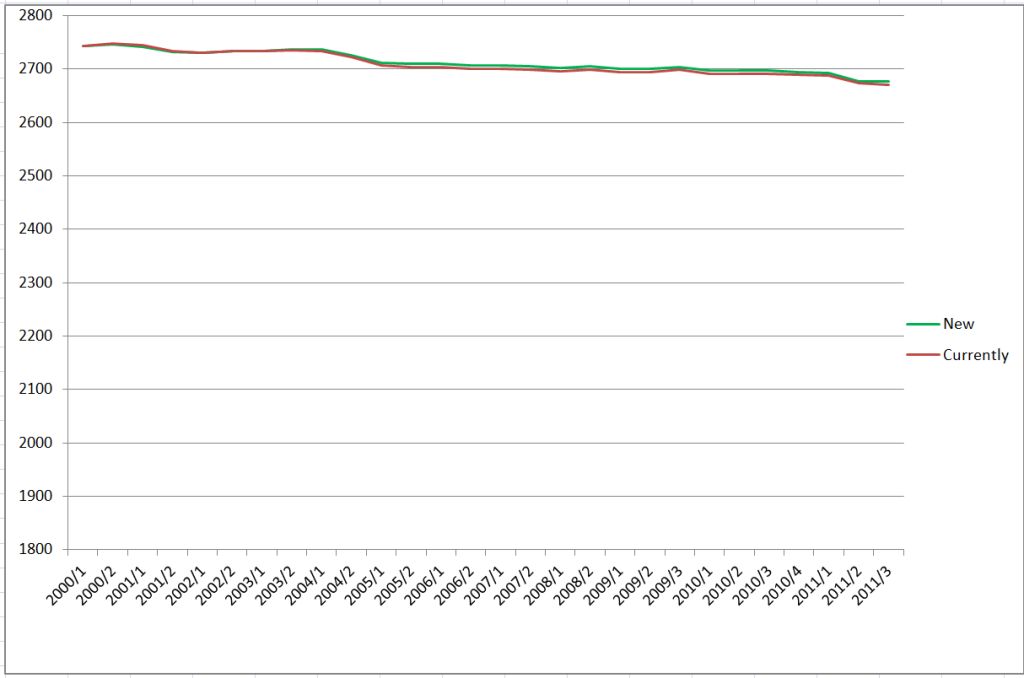
The following chart shows the avarage of fixed ratings for only those players who were on all ratinglists from 2000 to 2011 (constant player pool)
Using a constant player pool (4191 players) avoids the influence by changing the structure of players and shows the real development of the avarage fixed rating. Here we have a deflation of 46 points in 11 years, a fact which I observed in recent years. This is a weakness which affects categories and title norms. The new strategy would reduce this effect to 18 points in 11 years. This may be acceptable having in mind that all players of the selected pool became 11 years older during the considered period. Further development has to be watched carefully.

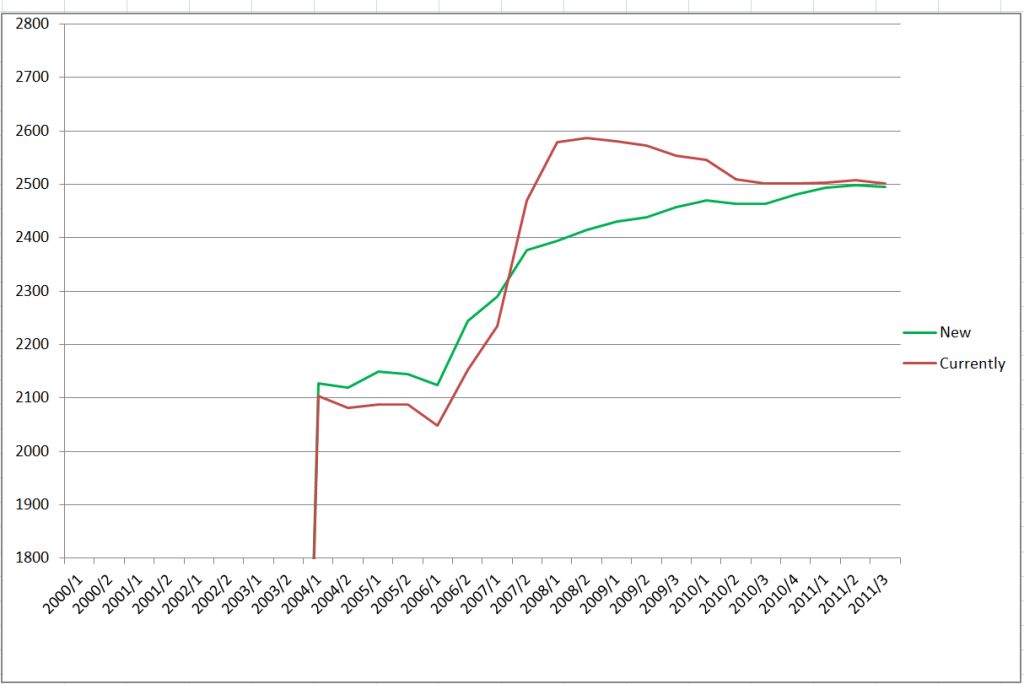
The chart shows the numbers of only those players who were active from 2000 to 2011 (grouped by range of 100 ratingpoints)
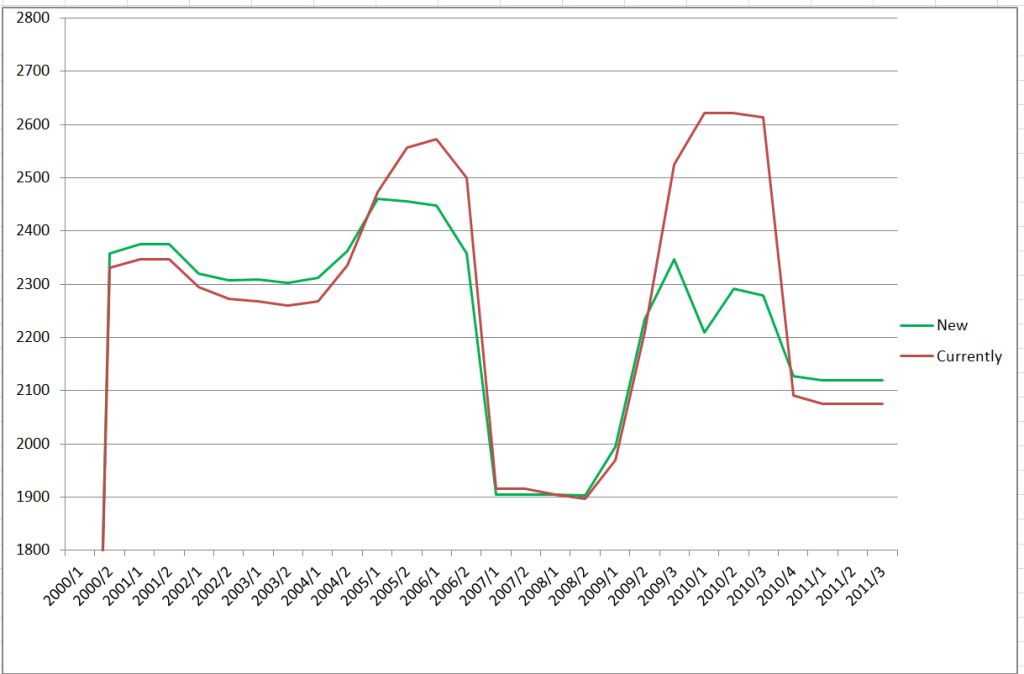
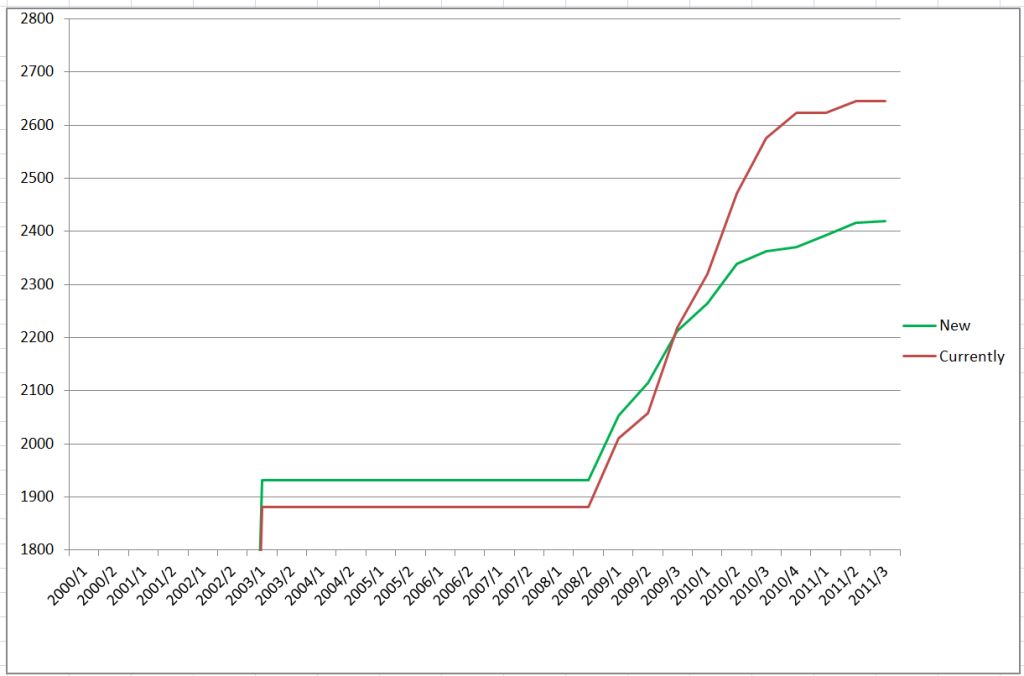
Charts above present comparison for a single player (just few examples)
===
Gerhard’s analysis above did generate quite a bit of discussion.
Summary
In summary, here were the items discussed and agreed to:
Present Situation
Ratings are calculated on the difference between players ratings set at the beginning of the tournament = start rating. The problem addressed is results of tournaments are spread over many rating periods with rating changes by players occurring.
Present Situation – Advantages
- All games within one tournament are treated equally
- The players know the effect on their ratings of any result at the beginning. It doesn’t matter when the game is finished.
Present Situation – Disadvantages
- New ratings are calculated by an increment to the base (last published rating) which is calculated using base-independent values. This leads to distortion.
- New players may have a too low start rating which damages the ratings of their opponents.
- The system may be abused by playing many games with artificially low start ratings.
- We have a significant deflation of average ratings during last 11 years.
Proposal
The rating difference is calculated by a new formula. For the player, the rating of the valid rating list at the end of the game is used. For the opponent, the higher value of his last rating and his start rating is used.
Proposal – Advantages
- The mix between base value and calculating the increment will be avoided.
- If an opponent’s rating goes up during the running time of a game, the player gets a more accurate probability; if an opponent’s rating goes dramatically down (normally due to other tournaments), his or her original strength is considered.
Proposal – Disadvantages
- Games in one tournament are treated different; the outcome depends on the time when a game is finished.
- Proposal – Considerations
- Possible delay in resigning or accepting draw by players who are staring at their ratings (called DMD).
- Possible inflation of average ratings by including a choice for a higher value.
Proposed Change to Tournament Rule 7.4
When a game is finished, the rating calculation procedure will use a player’s rating from the newest rating list for those players with a published rating; otherwise, the start rating is used. However, if a player’s current rating is lower than his start rating; the new ratings for his opponents are calculated using the player’s start rating.
Proposed Change to Rating Rules
The expected game result (We) is the percentage expectancy, obtained from item 4, based on the difference between the player’s rating and the opponent’s rating as defined in Tournament rule 7.4 (Rule number will be revised – this may change). If this difference is greater than 350, it is set to 350 for the evaluation.
A player without a published ICCF rating at the start of the tournament and without an applicable FIDE rating will be regarded as having a start rating equal to the tournament level (see item R 11 – Assumed start rating for a player without a published rating at the beginning of a tournament).
An additional change to Rule 7.7:
Players who do not qualify for a new rating because they have not finished a game during the evaluation period, remain on the active list because
- (a) they have finished a ratable game during the recent two calendar years, or
- (b) they are participating in at least one running tournament (rated or unrated).
Other players retain their most recent published rating, but are no longer shown in the published list. However, the webserver shows all players with their valid rating.
A proposal addendum was added by the Deputy Rating Commissioner, Mariusz Wojnar (POL) who recommended that the rating rules become part of the Tournament Rules (as an appendix). Also, he suggested that the Norms and Categories chart (always difficult to find) also be included in the Appendix to the Tournament Rules.
Implementation
ICCF Congress 2011 accepted above mentioned proposals, including the new rating calculations and modifications to the rating rules effective with the first rating period of 2012 (it means for games finished from 01.09.2011). The calculation programs were changed on the ICCF webserver in September 2011. Prediction option is following new rules, as well.